Bài viết này hệ thống lại bản chất của Dynamic Programming khi áp dụng trên cấu trúc đồ thị (graph). Tôi trình bày theo từng mục rõ ràng nhằm giúp người đọc hiểu trọng tâm và cách tiếp cận — đặc biệt phù hợp cho người mới học hoặc muốn ôn lại khái niệm.
1. Ý tưởng cốt lõi (Core Idea)
Trong các bài toán DP cổ điển (ví dụ: Fibonacci, Knapsack), các trạng thái thường có thứ tự tự nhiên từ 1 đến n. Trên đồ thị, mối quan hệ phụ thuộc giữa các đỉnh (nodes) không có thứ tự cố định, do đó cần xác định một thứ tự tính toán phù hợp để đảm bảo các phụ thuộc được thỏa mãn trước khi tính giá trị của một đỉnh.
Topological order là thứ tự các đỉnh của một đồ thị có hướng sao cho nếu tồn tại cạnh u → v thì u xuất hiện trước v. Nếu đồ thị là DAG (Directed Acyclic Graph), ta có thể thực hiện topological sort và dùng thứ tự này để làm DP một cách an toàn. Nếu đồ thị có chu trình (cycle), topological sort không khả dụng; trong trường hợp đó ta sử dụng các kỹ thuật khác như DFS kết hợp memoization hoặc thuật toán lặp relax kiểu Bellman–Ford / Floyd–Warshall cho tới khi các giá trị hội tụ.
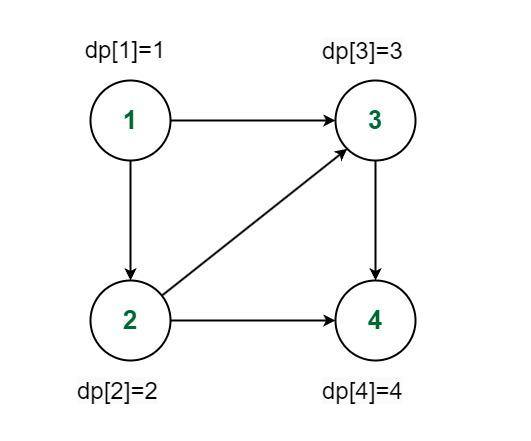
Ví dụ minh hoạ: để tính giá trị của đỉnh 4 (giả sử giá trị là tổng đường đi từ 1 đến 4), ta cần trước kết quả của các đỉnh 2 và 3; để có 2 và 3 ta phải có kết quả của 1. Vì vậy cần sắp xếp thứ tự sao cho mỗi đỉnh được tính sau các đỉnh mà nó phụ thuộc.
Cho ví dụ topo = [1, 2, 3, 4], ta sẽ tính như sau:
dp[1] = base
dp[2] = f(dp[1])
dp[3] = f(dp[1])
dp[4] = f(dp[2], dp[3])Như vậy thứ tự tính toán luôn đảm bảo các phụ thuộc đã có giá trị.
2. Ví dụ: Longest Path trên DAG
Bài toán: với n đỉnh và tập cạnh, tìm độ dài đường đi dài nhất trên một DAG. Ý tưởng: duyệt các đỉnh theo topological order và cập nhật giá trị cho các đỉnh kề.
Với mỗi cạnh u → v, thực hiện:
dp[v] = max(dp[v], dp[u] + 1)Pseudo code:
topo = topological_sort(graph)
dp = [0 for _ in range(n)]
for u in topo:
for v in graph[u]:
dp[v] = max(dp[v], dp[u] + 1)
return max(dp)Độ phức tạp thời gian: O(V + E) nếu đã có thứ tự topo. Topo đảm bảo không bao giờ cập nhật một đỉnh trước khi các tiền đề của nó đã được xử lý.
3. Khi đồ thị có chu trình (When Graph Has Cycles)
Nếu đồ thị chứa chu trình thì topological sort không khả dụng. Các phương án thay thế phổ biến:
- DFS + memoization: dùng DFS để tính giá trị theo nhu cầu, lưu kết quả (memo) để tránh tính lại. Với các bài toán yêu cầu đường đi dài nhất trên một đồ thị có chu trình, cần xử lý chu trình phù hợp (ví dụ phát hiện vô hạn hoặc cắt chu trình theo yêu cầu bài toán).
- Bellman–Ford / Floyd–Warshall: các thuật toán lặp relax qua các cạnh nhiều lần cho đến khi các giá trị hội tụ (hoặc xác định tồn tại chu trình âm với Bellman–Ford).
DFS + memo pseudo code:
def dfs(u):
if seen[u]:
return dp[u]
seen[u] = True
dp[u] = 1 + max(dfs(v) for v in graph[u])
return dp[u]Bellman–Ford: lặp qua tất cả cạnh V-1 lần, mỗi lần thực hiện cập nhật kiểu dist[v] = min(dist[v], dist[u] + w). Về bản chất đây là một dạng DP lặp (iterative relaxation) cho đến khi các giá trị ổn định.
4. Tương tự trong thực tế (Real-World Analogy)
Các bài toán quản lý phụ thuộc trong thực tế phản ánh chính xác tư duy DP trên đồ thị:
- Airflow DAG: một task chỉ chạy khi các task mà nó phụ thuộc đã hoàn thành.
- Dependency graph của trình biên dịch: module A phải được compile trước module B nếu B phụ thuộc A.
- Neural network forward pass: duyệt theo thứ tự topo của computation graph để tính giá trị các node.
Chung quy đây đều là các bài toán dependency resolution.
5. Kết luận chính (Key Takeaways)
- Trên DAG, ưu tiên dùng topo DP với độ phức tạp O(V + E).
- Nếu đồ thị có chu trình, cân nhắc dùng DFS + memoization hoặc thuật toán lặp relax như Bellman–Ford.
- Trọng tâm không phải công thức; mà là quản lý luồng thông tin (dependency) và thứ tự tính toán.
- DP trên đồ thị = reuse (tái sử dụng kết quả) + ordering (sắp xếp thứ tự) + dependency control (kiểm soát phụ thuộc).
6. Bài tập liên quan (Related LeetCode Problems)
Để luyện tập, có thể tham khảo các bài sau (từ dễ đến trung bình–khó):
- 207. Course Schedule — phát hiện chu trình + topo sort
- 210. Course Schedule II — xây dựng topo order
- 329. Longest Increasing Path in a Matrix — DP trên graph ẩn trong grid
- 1514. Path with Maximum Probability — DP kết hợp Dijkstra
- 787. Cheapest Flights Within K Stops — biến thể của Bellman–Ford
7. Nhận xét cá nhân (Personal Reflection)
Trước đây tôi từng hiểu DP là tập hợp các công thức chuyển trạng thái cứng nhắc. Sau khi tiếp cận sâu hơn, nhận ra bản chất của DP là quản lý luồng thông tin trong một mạng phụ thuộc. Đồ thị chỉ làm cho khái niệm trừu tượng hơn, nhưng nguyên lý vẫn là: tính các phần dễ trước, lưu kết quả, rồi sử dụng để tính phần phức tạp hơn.
Khi nắm được nguyên lý này, các thuật toán như Bellman–Ford, Floyd–Warshall hay topo DP trở nên trực quan hơn. Thói quen hữu ích: vẽ dependency graph trước khi code và thử nghiệm với ví dụ nhỏ (4–5 đỉnh) để quan sát thứ tự và cách giá trị lan truyền.
Nguyên tắc thực hành:
- Hiểu luồng tính toán (simulate flow) trước khi triển khai code — Understand > Memorize.
- DP = reuse + ordering + dependency management — từ đó có thể tái cấu trúc thuật toán mà không cần thuộc lòng công thức.
- Nếu có chu trình, không cố ép topo sort; chuyển sang phương pháp cập nhật lặp như Bellman–Ford và tiếp tục relax cho tới khi ổn định.
- Luôn xác định rõ “ai phụ thuộc vào ai” — trực quan hoá giúp nắm nhanh dependency.
- Bắt đầu từ base case; suy nghĩ theo hướng tiến (past → future) hoặc lùi (goal → start) tuỳ bài toán.
- Nếu thấy tính đi tính lại cùng một giá trị — dùng memoization; kiểm tra kỹ biên (boundaries) và base case để tránh lỗi phổ biến.
Ghi chú: Đây là chia sẻ từ góc nhìn người bắt đầu nhằm giúp người học hệ thống lại kiến thức. Việc thực hành và giải nhiều bài sẽ giúp nâng cấp khả năng làm chủ các biến thể nâng cao hơn.
